Linear Transformation

Linear transformations are a foundational concept in linear algebra. To make the idea stick, I’ll start with an intuitive explanation before introducing the formal definition. That way, the formalism won’t distract from the core idea.

So, what exactly is a linear transformation?

Let’s first focus on the word transformation. Think of it as a kind of function — one that takes an input vector and returns an output vector. We use the word transformation rather than just function because it evokes a sense of motion or change. Imagine an input vector moving or morphing into its output counterpart. Now, zoom out and imagine this happening to every possible vector in your space — each one being “moved” to a new position by the transformation. It’s like the entire space is being reshaped.

Picture a transformation as stepping through a portal where the world looks completely different on the other side — flipped, rotated, stretched. That’s the kind of effect transformations can have. Some transformations can be wild — they might bend, twist, or distort space in bizarre ways. But in linear algebra, we narrow our focus to a special kind: linear transformations.

Linear transformations are more structured and obey specific rules. Visually, they don’t tear or bend space. Here’s what makes a transformation linear:

1. The origin stays fixed — it always maps to itself.
2. Lines remain lines — a straight line going in becomes a straight line coming out. The line might get stretched, compressed, or rotated, but it doesn’t bend or curve.
3. Gridlines stay evenly spaced — imagine a grid on the xy-plane. A linear transformation can shear, rotate, scale, or reflect the grid, but it will still look like a regular grid. Parallel lines stay parallel, and straightness is preserved.
4. Proportions are consistent along lines — for example, if you double the length of a vector before applying the transformation, the output will also double compared to the original transformed vector.

In short, linear transformations can scale, rotate, reflect, or shear the space — but they always preserve the essential structure of that space. They respect straightness, proportionality, and the central role of the origin.

Numerical Representation

Imagine you’re blindfolded and can’t visually track where each vector lands after the transformation. In this case, a numerical representation becomes incredibly useful. Picture it like a “box” with numbers — this box represents the transformation. You input your vector, the box performs some calculations, and it outputs the resulting vector.

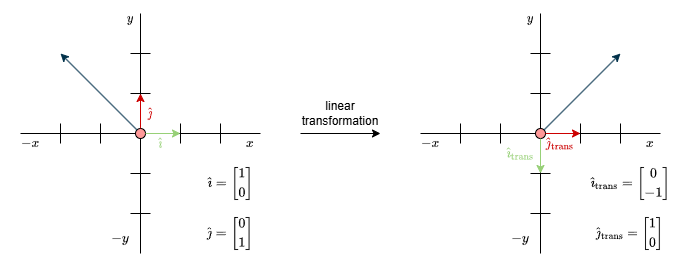
To create this numerical representation, all you need to do is determine where the basis vectors land after the transformation. (This makes sense because we use these basis vectors to construct all the other vectors in the space anyway) Since the transformation is linear, we can express any vector as a linear combination of the transformed basis vectors, like this:

(For this example, I’ve chosen a 90° clockwise rotation. That means the unit vector \(\hat{\imath}\) in the \(x\) direction rotates into the negative \(y\)-direction, and the \(\hat{\jmath}\)​ in the \(y\) direction ends up in the positive \(x\)-direction.)

\(\begin{align*}\mathbf{v} &= x \cdot \hat{\imath}_{\text{trans}} + y \cdot \hat{\jmath}_{\text{trans}} \\\\ &= x \cdot \begin{bmatrix} 0 \\ -1 \end{bmatrix} + y \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix}\end{align*}\)

Now that we understand how the transformation works, we can plug in any coordinates \(x\) and \(y\) for a vector and immediately know where it ends up. It’s pretty amazing that this whole space-changing process can be captured using just four numbers.

But let’s be honest—writing out the full linear combination every time gets old fast, especially when we start working in higher dimensions with lots of vectors. That’s where a new, simpler notation comes in: the matrix.

A matrix neatly bundles the transformed basis vectors into a small grid of numbers:

\(\begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix}\)

This one’s a 2×2 matrix, meaning it has 2 rows and 2 columns. (It’s always rows first, then columns, unless otherwise noted.) Each column in the matrix represents a basis vector:

• The first column shows what happens to the basis vector in the \(x\)-direction.
• The second column shows what happens to the basis vector in the \(y\)-direction.

The rows just tell you the actual coordinates:

• The first row gives the \(x\)-components.
• The second row gives the \(y\)-components.

This is the “box of numbers” we talked about earlier. Now, instead of writing everything out by hand, we can just multiply our input vector by this matrix and get the result in one step.

Let’s now generalize this idea so it works with any transformation. Mathematically, that looks like this:

\(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \mathbf{v} =\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix} a \\ b \end{bmatrix} + y \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}\)

You might have seen this formulation before—it’s called vector-matrix multiplication. Like many others, myself included, we were often told to memorize this rule and apply it to exercises in college without truly understanding what it meant. Thankfully, now we have a clearer understanding of what this represents. Each column of the matrix corresponds to a transformed basis vector. When we multiply the matrix by a vector, we’re essentially transforming that vector, moving it according to the transformation described by the matrix.

Matrix Multiplication

We’ve already seen how we can apply transformations like rotation, skewing, and so on to vectors using linear transformations. But what if we want to apply multiple transformations?

One way to do that is to apply them one after the other, like this (Let’s say we apply a 90° clockwise rotation followed by a skew and we use some random input vector \(\mathbf{v}\)):

\( \begin{align*} &= \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix} \left( \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix} \mathbf{v} \right) \\\\ &= \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \left( \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix} \begin{bmatrix} 5 \\ 10 \end{bmatrix} \right) \\\\ &= \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 10 \\ -5 \end{bmatrix} \\\\ &= \begin{bmatrix} 5 \\ -5 \end{bmatrix}\end{align*}\)

But couldn’t we just create a single transformation that does the job of both? In other words, is it possible to build one matrix that captures the combined effect of applying two transformations in sequence—so we only need to apply one?

The answer is yes. This new matrix is called a composition matrix, because it’s composed of the two transformations we want to combine. So, how do we compute it?

We use the same trick we’ve been using—we look at where the basis vectors end up. We already know that each column of a matrix shows where a basis vector lands after a transformation. So to find the composition matrix, we take each column (each transformed basis vector), treat it like a regular vector, and apply matrix-vector multiplication just like we did before. In mathematical terms, it looks like this:

\(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} {\color{red} e} & {\color{blue} f}\\ {\color{red} g} & {\color{blue} h} \end{bmatrix} = \) ?

\( \begin{align*} & \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} {\color{red} e} \\ {\color{red} g} \end{bmatrix} \\\\ &= \begin{bmatrix} {\color{black} {ae}} + {\color{black} {bg}} \\ {\color{black} {ce}} + {\color{black} {dg}} \end{bmatrix} \end{align*} \)

\( \begin{align*} & \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} {\color{blue} f} \\ {\color{blue} h} \end{bmatrix} \\\\ &= \begin{bmatrix} a{\color{black} f} + b{\color{black} h} \\ c{\color{black} f} + d{\color{black} h} \end{bmatrix} \end{align*} \)

\( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix}\)

Whenever you come across matrix multiplication—which happens a lot in machine learning—just remember that it represents a combination of transformations. It’s like two separate movements unified into one.