Linear Combination

When you see a vector written as numbers — say, \( \mathbf{v} = \begin{bmatrix} 14 \\ 2 \end{bmatrix}\) — you can think of it as taking 14 steps to the right and 2 steps upward, as we discussed earlier. But there’s another way to look at those numbers: they are scalars, used to scale certain vectors. To make the idea of “moving right” and “moving up” more concrete, let me introduce two special vectors called standard unit vectors, usually written as \(\hat{\imath}\) and \(\hat{\jmath}\).

(A unit vector is a vector with a magnitude (or length) of exactly 1. It is considered “standard” because it points in the direction of one of the coordinate axes in a given space.)

• \(\hat{\imath}\) represents one unit in the x-direction (right).
• \(\hat{\jmath}\) represents one unit in the y-direction (up).

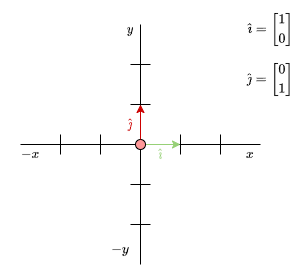
Using these, we can now express the vector \(\mathbf{v}\) like this:

\(\mathbf{v} = 14 \hat{\imath} + 2 \hat{\jmath}\)

This means we scale \(\hat{\imath}\) by 14 and \(\hat{\jmath}\) by 2, and then add them together to get the vector \(\mathbf{v}\). The cool part is that any vector can be written this way — as a combination of these vectors scaled by appropriate numbers. Expressing a vector by scaling and adding other vectors — as we did above — is called a linear combination.

This brings us to a powerful idea:

Can we choose different vectors instead of î and ĵ to represent our space?

Yes—but you have to be careful. For example: If we decide to use different vectors, like:

\(\mathbf{c} = \begin{bmatrix} 5 \\ 3 \end{bmatrix} \)

\(\mathbf{d} = \begin{bmatrix} 7 \\ 2 \end{bmatrix} \)

to describe other vectors, then \(\mathbf{v}\) will point to a completely different vector than it would if we were using the usual \(\hat{i}\) and \(\hat{j}\):

\( \begin{align*} \mathbf{v} &= 14 \mathbf{c} + 2 \mathbf{d} \\ \\ &= 14 \begin{bmatrix} 5 \\ 3 \end{bmatrix}+ 2\begin{bmatrix} 7 \\ 2 \end{bmatrix} \\ \\ &= \begin{bmatrix} 70 \\ 42 \end{bmatrix} + \begin{bmatrix} 14 \\ 4 \end{bmatrix} \\ \\ &= \begin{bmatrix} 84 \\ 46 \end{bmatrix} \end{align*} \)

Compared to:

\( \begin{align*} \mathbf{v} &= 14 \hat{\imath} + 2 \hat{\jmath} \\ \\ &= 14 \begin{bmatrix} 1 \\ 0 \end{bmatrix}+ 2\begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ \\ &= \begin{bmatrix} 14 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 2 \end{bmatrix} \\ \\ &= \begin{bmatrix} 14 \\ 2 \end{bmatrix} \end{align*} \)

The numbers \(\begin{bmatrix} 14 \\ 2 \end{bmatrix}\) tell us how much of each of two specific vectors we’re using to build another vector. But these numbers alone don’t tell the full story—what they describe depends entirely on the two original vectors used in the construction. The same coordinates can represent very different actual vectors in space, depending on the direction and length of the vectors being combined.

Think of it like this: imagine giving directions using steps—”14 steps forward and 2 steps right.” How far you actually go depends on how long each step is. If one person uses tiny steps and another uses giant ones, they end up in very different places even if they follow the same instructions.

So, when we describe a vector using coordinates like \(\begin{bmatrix} 14 \\ 2 \end{bmatrix}\), we’re implicitly assuming a specific set of vectors that we’re combining. Without knowing what those original vectors are, we can’t know exactly what the final vector looks like in space. If we change the vectors we’re using to construct others, the numbers (coordinates) change—even though the actual result, the vector itself, stays the same.

Span

When you pick two vectors, the span refers to all the vectors you can create by combining them—scaling them and adding them together in every possible way. For example, if you use the standard unit vectors \(\hat{\imath}\) and \(\hat{\jmath}\), their span covers the entire 2D space; in other words, you can reach any 2D vector using just those two. To put it more formally and generally:

Linear Independence

For most sets of vectors, it’s possible to construct any other vector in the space using a linear combination of those vectors. In 2D, for example, you need two vectors to span the entire plane. In 3D, you need three vectors, and in 4D, four vectors—you get the idea.

The key word here is most. If you’re unlucky and choose two vectors in 2D that lie along the same line—meaning one is just a scaled version of the other—then you’re limited. In that case, any linear combination of the two will still fall along that same line. You won’t be able to reach points outside of it, which means you’re not spanning the whole 2D space.

In other words, if one vector is simply a multiple of another, it’s redundant—it doesn’t contribute anything new. You can remove it without losing the ability to generate any additional vectors. When this happens, the vectors are called linearly dependent—because one can be written as a linear combination of the others.

On the other hand, if removing a vector does reduce the span—meaning you can no longer reach as many directions in the space—then that vector is linearly independent. It brings something essential to the table: a new direction, a new dimension. Without it, your set can’t cover the entire space.

The same idea extends naturally to higher dimensions. For example, in 3D space, if you have three vectors and one of them lies in the span (plane in 3D) defined by the other two, then it doesn’t contribute anything new. It can already be formed by a linear combination of the other two, so it’s considered linearly dependent.

Basis

Now that we’ve explored the concepts of linear independence and the span of vectors, we can introduce the formal definition of a basis (or basis vectors) for a vector space:

Throughout this discussion, I’ve referred to vectors being used to “create” other vectors through linear combinations. If a set of vectors can span the entire space—say, all possible vectors in 2D—and they are linearly independent, then that set is a basis.

I’ve held off on using the term basis until now because it’s crucial that the vectors not only span the space but are also linearly independent. If, for example, you have two vectors in 2D that are linearly dependent, their span would only form a line, not the full 2D space. In that case, they wouldn’t qualify as a basis.

So, whenever you’re combining vectors to generate others, make sure they’re linearly independent before calling them a basis.